Skip to contents

Real Data Analysis Example 2

Dongyuan Song

Bioinformatics IDP, University of California, Los Angeles

Lehan Zou

Dertment of Statistics, University of California, Los Angeles

Shiyu Ma

Department of Statistics, University of California, Los Angeles
Source: vignettes/RealDataAnalysis2.Rmd
RealDataAnalysis2.Rmd

Real Data Analysis Example 2

scGTM identifies informative gene expression trends after immune cell stimulation.

As in the second real data example, we use the scGTM to categorize gene expression trends in mouse dendritic cells(DCs) after simulation with lipopolysaccharide (LPS).

LPS_sce <- read_csv("LPS data.csv")
## Rows: 390 Columns: 4018
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## chr    (1): Unnamed: 0
## dbl (4017): pseudotime, CCL5, CXCL10, LYZ2, CCL4, IL12B, CCL22, IL1B, LYZ1, ...
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
Poisson_para <- read_csv("Poisson_para.csv")
## New names:
## Rows: 4016 Columns: 26
## ── Column specification
## ──────────────────────────────────────────────────────── Delimiter: "," chr
## (2): gene_index, Fisher dbl (19): ...1, negative_log_likelihood, mu, k1, k2,
## t0, t0_lower, t0_upper,... lgl (5): phi, sd, alpha, beta, Design_para
## ℹ Use `spec()` to retrieve the full column specification for this data. ℹ
## Specify the column types or set `show_col_types = FALSE` to quiet this message.
## • `` -> `...1`
gene_counts <- LPS_sce %>% dplyr::rename(cell_id = `Unnamed: 0`)
gene_counts <- gene_counts  %>% tidyr::pivot_longer(!c("pseudotime", "cell_id"), names_to = "gene") %>% dplyr::mutate(`log(count+1)` = log1p(value))

Poisson 

Poisson_para %>% dplyr::group_by(Transform) %>% dplyr::summarise(n())
## # A tibble: 2 × 2
##   Transform `n()`
##       <dbl> <int>
## 1         0  2341
## 2         1  1675

Cal intercept model 

LPS_counts <- LPS_sce %>% dplyr::select(-c("Unnamed: 0", "pseudotime")) %>% t()
pseudotime <- LPS_sce$pseudotime
Poisson_loglik <- apply(LPS_counts, 1, function(gene) {
  fit <- mgcv::gam(gene ~ 1, family = "poisson")
  -logLik(fit)})

Select significant genes 

Poisson_new <- Poisson_para %>% dplyr::mutate(nzp = rowMeans(LPS_counts!=0))%>% dplyr::mutate(Poisson_para, nllik = Poisson_loglik) %>% dplyr::mutate(llk_diff = 2*(nllik - negative_log_likelihood)) %>% dplyr::arrange(desc(llk_diff)) %>% dplyr::mutate(pvalue = pchisq(llk_diff, 3, lower.tail = FALSE)) %>% dplyr::mutate(adj_pvalue = p.adjust(pvalue, "BH")) %>% dplyr::filter(adj_pvalue < 0.01)
Poisson_new
## # A tibble: 2,338 × 31
##     ...1 gene_index negative_…¹    mu    k1     k2    t0 phi   sd    alpha beta 
##    <dbl> <chr>            <dbl> <dbl> <dbl>  <dbl> <dbl> <lgl> <lgl> <lgl> <lgl>
##  1   918 GU332589       191392.  8.99 0.210  8.60  0.772 NA    NA    NA    NA   
##  2     1 CCL5           191664. 11.1  7.88   0.912 0.792 NA    NA    NA    NA   
##  3     9 GM11428        217635. 10.7  0.176 36.6   0.623 NA    NA    NA    NA   
##  4     3 LYZ2           211794. 11.1  0.354 16.5   0.575 NA    NA    NA    NA   
##  5  3034 ACTB             1287.  2.29 2.18  21.5   0.579 NA    NA    NA    NA   
##  6   171 CST3            10165.  4.53 1.69  33.3   0.608 NA    NA    NA    NA   
##  7   358 FTH1           221830. 10.4  0.296 13.3   0.750 NA    NA    NA    NA   
##  8    14 CCL17           47407.  4.00 3.13   3.50  0.519 NA    NA    NA    NA   
##  9  1695 AK140265       161029.  8.27 0.152  5.24  0.652 NA    NA    NA    NA   
## 10  2003 FTL1           214900. 10.4  7.83   0.536 0.296 NA    NA    NA    NA   
## # … with 2,328 more rows, 20 more variables: t0_lower <dbl>, t0_upper <dbl>,
## #   t0_std <dbl>, k1_lower <dbl>, k1_upper <dbl>, k1_std <dbl>, k2_lower <dbl>,
## #   k2_upper <dbl>, k2_std <dbl>, mu_lower <dbl>, mu_upper <dbl>, mu_std <dbl>,
## #   Fisher <chr>, Transform <dbl>, Design_para <lgl>, nzp <dbl>, nllik <dbl>,
## #   llk_diff <dbl>, pvalue <dbl>, adj_pvalue <dbl>, and abbreviated variable
## #   name ¹​negative_log_likelihood
gene_counts <- gene_counts %>% dplyr::filter(gene %in% Poisson_new$gene_index)

Convert gene name 

Poisson_new <- Poisson_new %>% mutate(gene_index = sapply(gene_index, function(x) {
  gene <- str_split(x, "-")[[1]]
  if(length(gene) > 1) {
    gene <- str_to_title(gene)
    gene <- paste(gene[1], gene[2], sep = "-")
  } else {
    gene <- str_to_title(gene)
    
  }
  gene <- gsub("rik", "Rik", gene)
  gene
})) 

gene_counts <- gene_counts %>% mutate(gene = sapply(gene, function(x) {
  gene <- str_split(x, "-")[[1]]
  if(length(gene) > 1) {
    gene <- str_to_title(gene)
    gene <- paste(gene[1], gene[2], sep = "-")
  } else {
    gene <- str_to_title(gene)
    
  }
  gene
}))
Poisson_mat <-Poisson_new %>% dplyr::select(-c("...1", "gene_index", "negative_log_likelihood", "phi", "pvalue", "Fisher", "k1_std","k2_std","mu_std")) %>% as.matrix()

Plot curve 

gene_curve <- function(t, mu, k1, k2, t0) {
  if(t <= t0) v <- mu*exp(-k1*(t-t0)^2)
  else v <- mu*exp(-k2*(t-t0)^2)
  v
}
gene_predict <- function(gene, pseudotime) {
  i = Poisson_new %>% dplyr::filter(gene_index == gene) %>% as.vector()
  res <- gene_curve(t = pseudotime, mu = as.numeric(i[4]), k1 = abs(as.numeric(i[5])), k2 = abs(as.numeric(i[6])), t0 = as.numeric(i[7]))
  res
}
gene_predict2 <- function(gene_use, pseudotime) {
  i = Poisson_new %>% dplyr::filter(gene_index == gene_use) %>% as.vector()
  gene_max <- gene_counts %>% group_by(gene) %>% dplyr::summarise(max_value = max(`log(count+1)`)) %>% dplyr::filter(gene == gene_use) %>% .$max_value
  res <- gene_curve(t = pseudotime, mu = as.numeric(i[4]), k1 = abs(as.numeric(i[5])), k2 = abs(as.numeric(i[6])), t0 = as.numeric(i[7]))
  gene_max - res
}

Add scKGAM prediction 

gene_counts <- gene_counts %>% dplyr::filter(gene %in% Poisson_new$gene_index)

we use the scGTM’s confidence levels of the three parameters \(t_0\) , \(k_1\) , and \(k_2\) to categorize the 2405 genes into three types: 1) hill-shaped and mostly increasing genes 2) hill-shaped and mostly decreasing genes 3) valley-shaped genes ### Plot some genes

gene_vec1 <- Poisson_new %>% dplyr::arrange(desc(llk_diff)) %>% dplyr::filter(Transform == 0) %>% dplyr::filter(t0_lower > 0.6 & k1_lower > 1)%>% dplyr::arrange(desc(nzp))

gene_vec <- gene_vec1$gene_index[1:5]
p1 <- gene_counts %>% dplyr::filter(gene %in% gene_vec) %>% dplyr::mutate(prediction = mapply(gene = gene, pseudotime  = pseudotime, FUN = gene_predict)) %>% dplyr::mutate(gene = factor(gene, levels = gene_vec)) %>% ggplot(aes(x = pseudotime, y = `log(count+1)`)) +geom_point(size = 1, alpha = 0.3) + geom_line(aes(y = prediction), color = "blue") + facet_wrap(~gene, scales = "free_y", nrow = 1) +theme(aspect.ratio = 1) + ggtitle("Hill-shaped Genes (Mostly Increasing)")
p1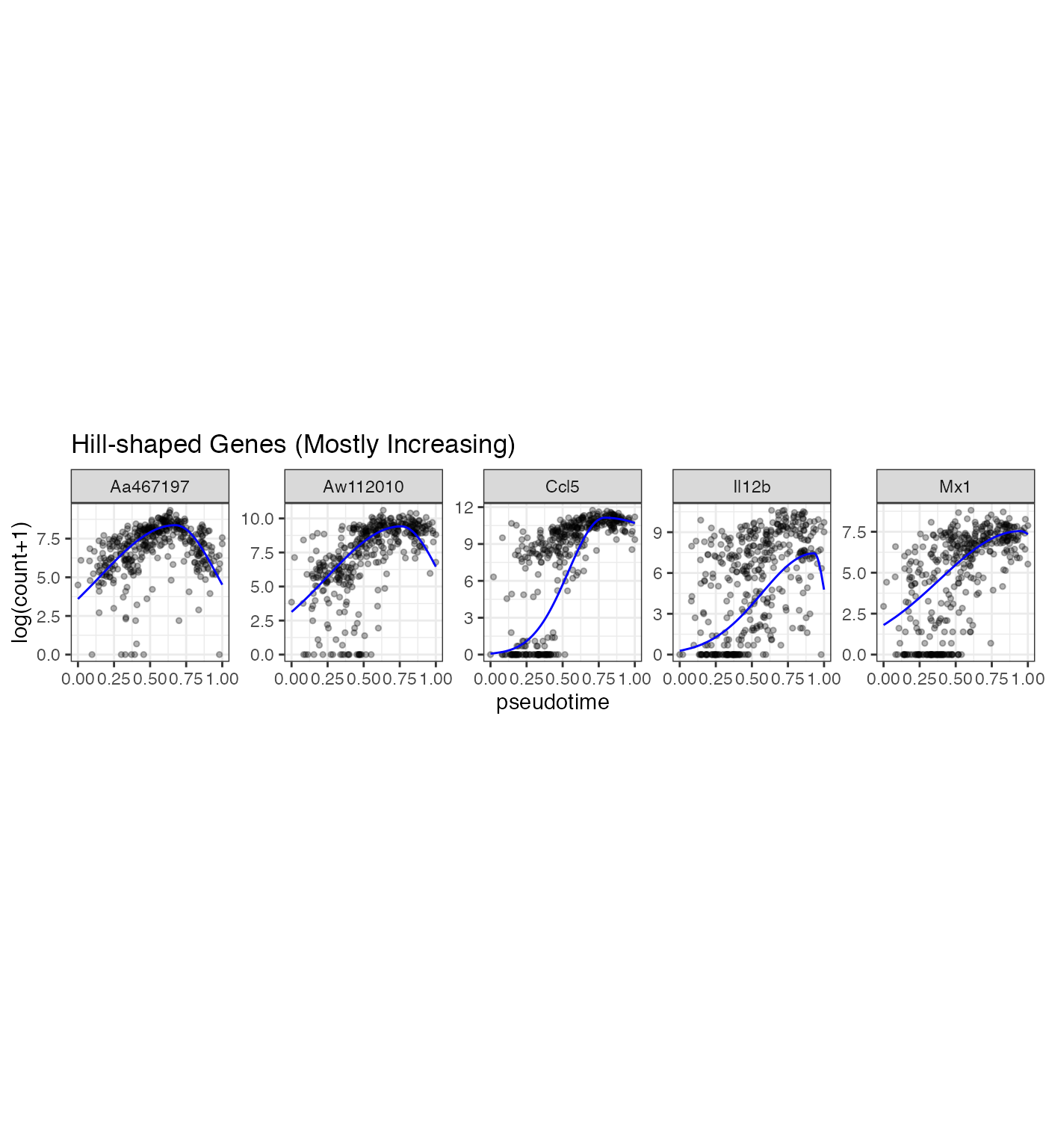

gene_vec2 <- Poisson_new %>% dplyr::arrange(desc(llk_diff)) %>% dplyr::filter(Transform == 0) %>% dplyr::filter(t0_upper < 0.4 & k2_lower > 1) %>% dplyr::arrange(desc(nzp))

gene_vec <- gene_vec2$gene_index[1:5]
p2 <- gene_counts %>% dplyr::filter(gene %in% gene_vec) %>% dplyr::mutate(prediction = mapply(gene = gene, pseudotime  = pseudotime, FUN = gene_predict)) %>% dplyr::mutate(gene = factor(gene, levels = gene_vec)) %>% ggplot(aes(x = pseudotime, y = `log(count+1)`)) +geom_point(size = 1, alpha = 0.3) + geom_line(aes(y = prediction), color = "blue")  + facet_wrap(~gene, scales = "free_y", nrow = 1) +theme(aspect.ratio = 1) +ggtitle("Hill-shaped Genes (Mostly Decreasing)")
p2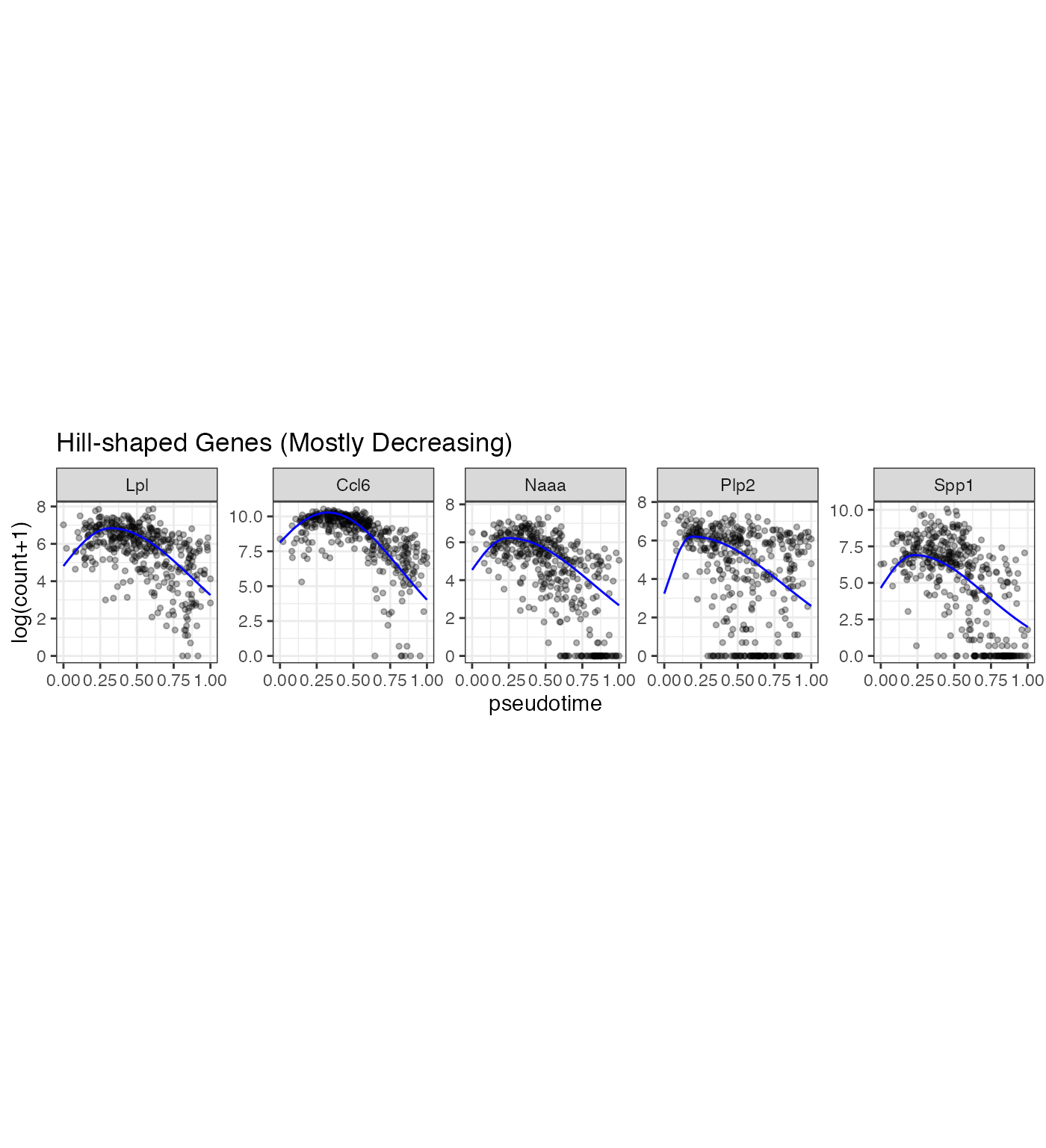

gene_vec3 <- Poisson_new %>% dplyr::arrange(desc(llk_diff)) %>% dplyr::filter(Transform == 1) %>% dplyr::filter(k1_lower > 1 & k2_lower > 1)%>% dplyr::arrange(desc(nzp))

gene_vec<- gene_vec3$gene_index[1:5]
p3 <- gene_counts %>% dplyr::filter(gene %in% gene_vec) %>% dplyr::mutate(prediction = mapply(gene_use = gene, pseudotime  = pseudotime, FUN = gene_predict2)) %>% dplyr::mutate(gene = factor(gene, levels = gene_vec)) %>% ggplot(aes(x = pseudotime, y = `log(count+1)`)) +geom_point(size = 1, alpha = 0.3) + geom_line(aes(y = prediction), color = "blue")  + facet_wrap(~gene, scales = "free_y", nrow = 1) +theme(aspect.ratio = 1) +ggtitle("Valley-shaped Genes")
p3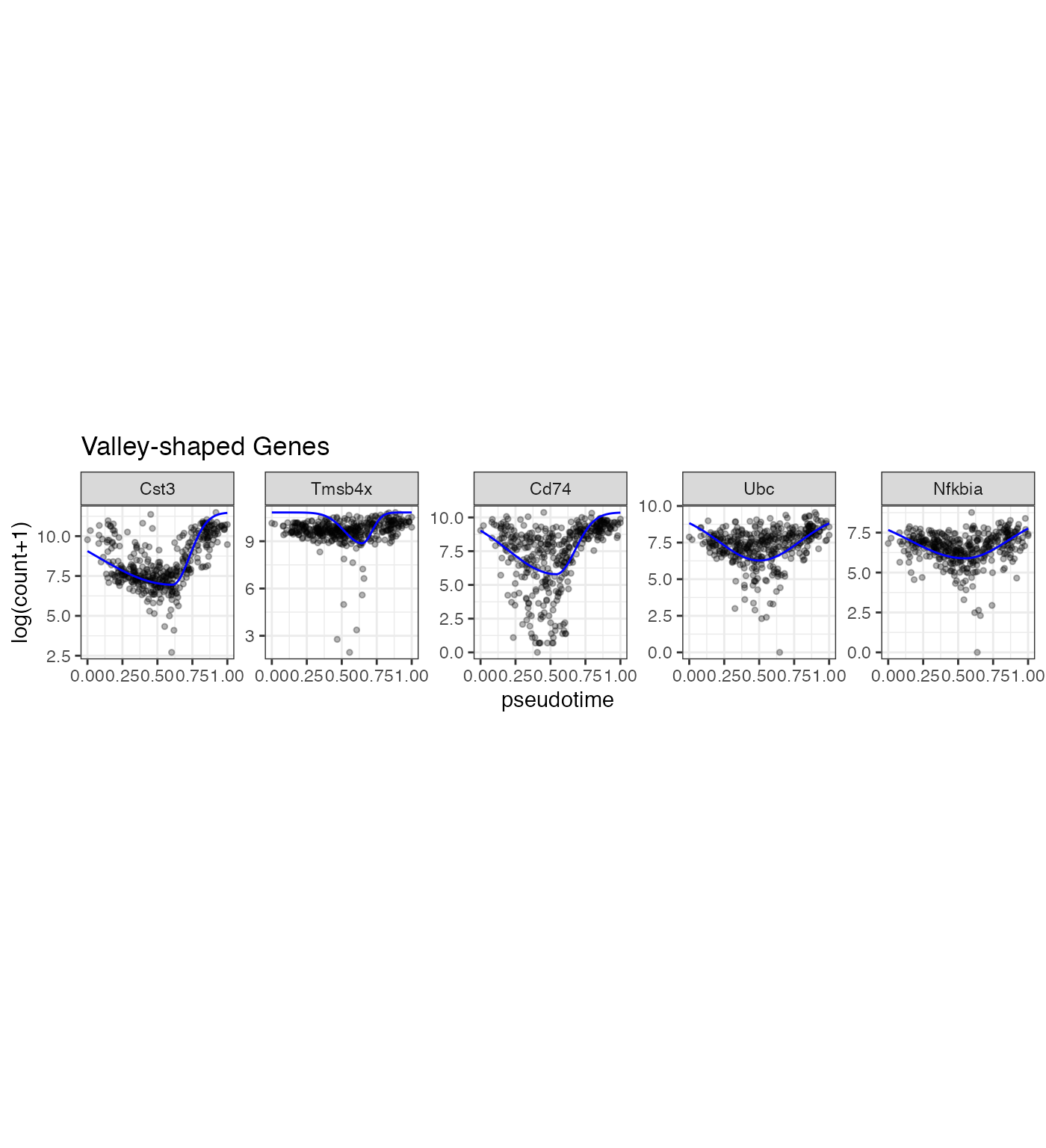

gcSample <- list(`Mostly Increasing` = gene_vec1$gene_index, `Mostly Decreasing` = gene_vec2$gene_index, `Valley-shaped` = gene_vec3$gene_index)

ck <- compareCluster(geneCluster = gcSample, fun = enrichGO,
                      OrgDb         = org.Mm.eg.db,
                      ont           = "BP",
                pAdjustMethod = "BH",
                pvalueCutoff  = 0.01,
                qvalueCutoff  = 0.05,
                keyType       = "SYMBOL",
                maxGSSize = 500)

ck2 <- clusterProfiler::simplify(ck, cutoff = 0.6)
p_go <- clusterProfiler::dotplot(ck2, showCategory = 10, font.size = 12, label_format = 30)
p_go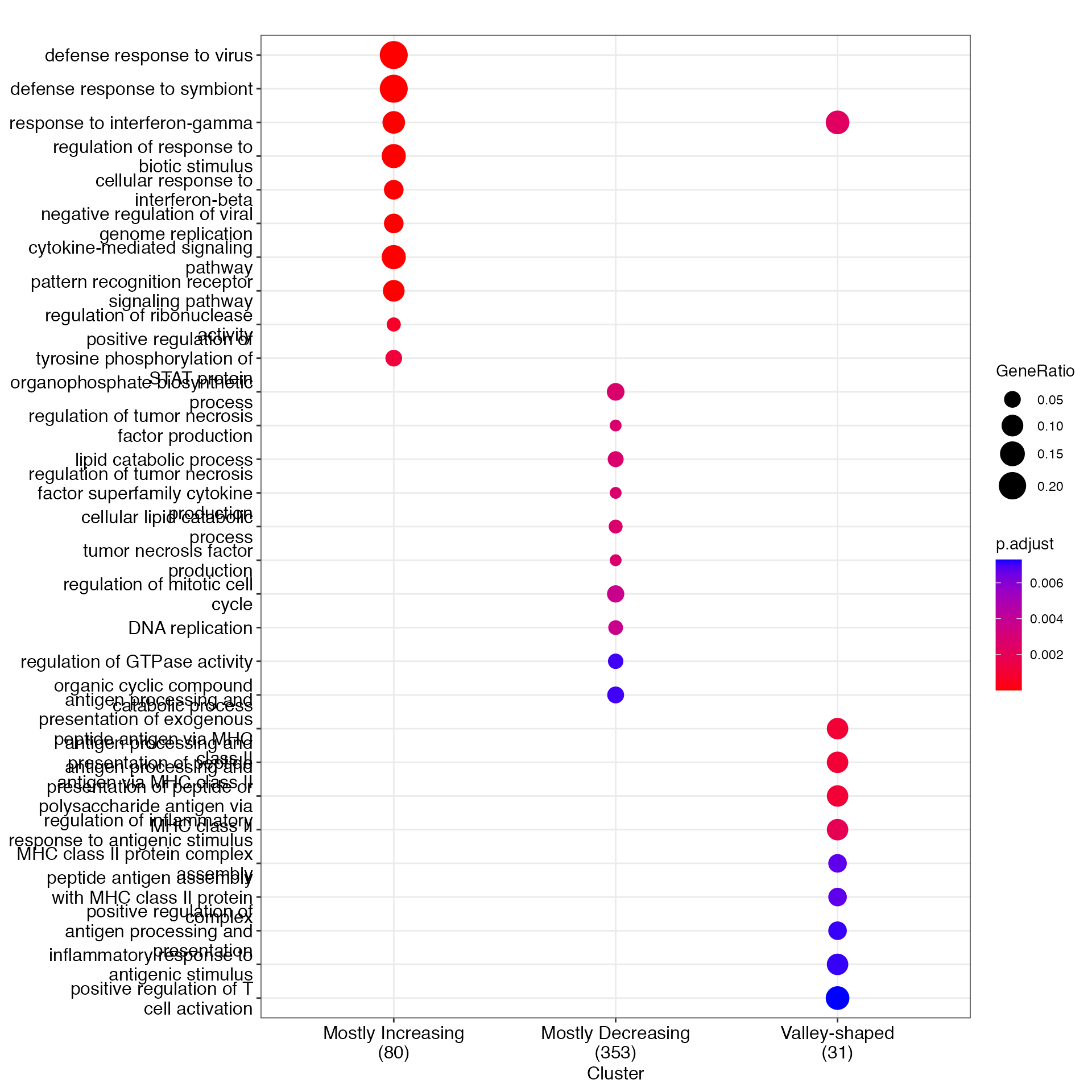

p_gene_trend <- ggpubr::ggarrange(p1, p2, p3, ncol = 1, align = "hv")
p_gene_trend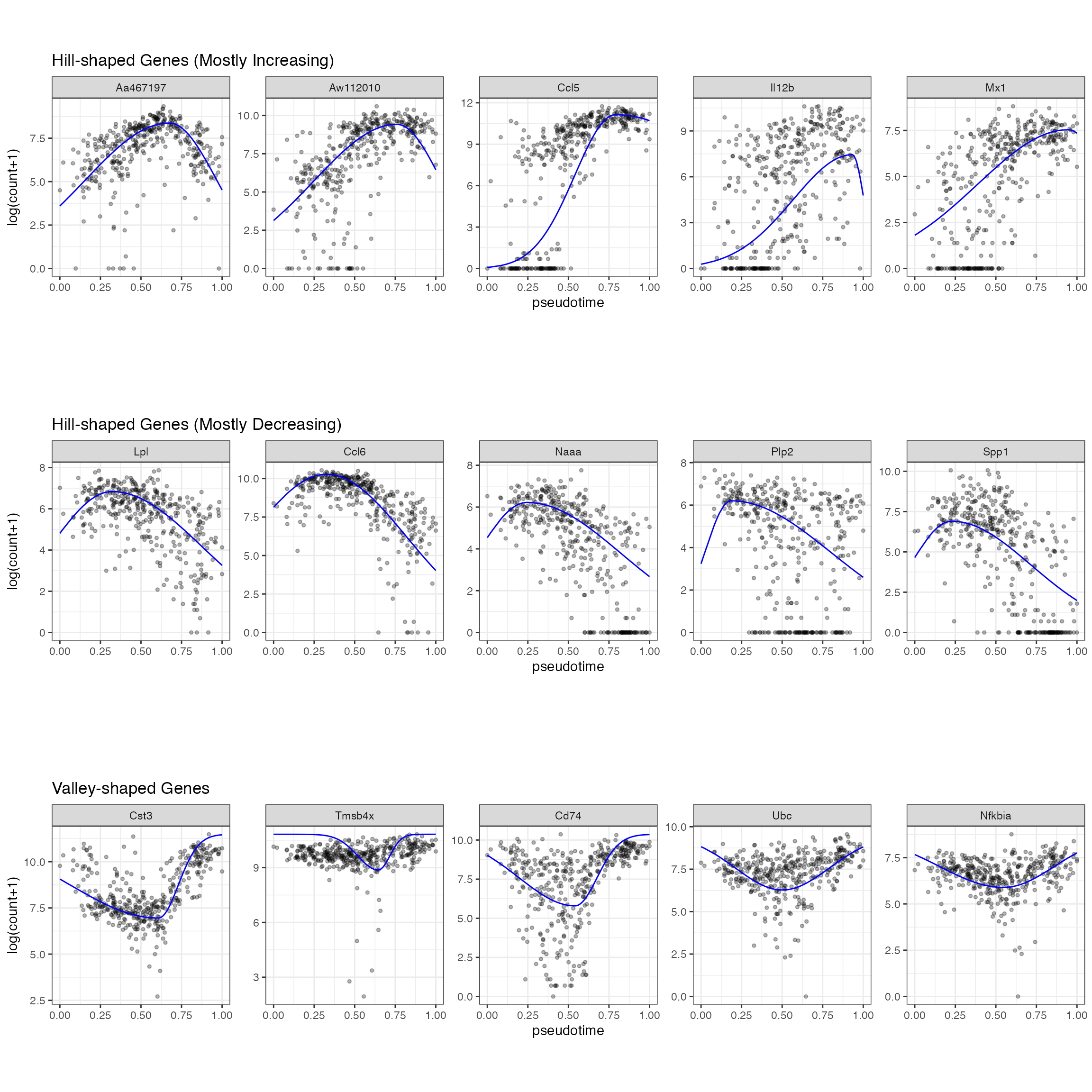

p_LPS <- ggpubr::ggarrange(p_go, p_gene_trend, ncol = 1, heights = c(8, 5), align = "h", labels = c("a", "b"), font.label = list(size = 20, face = "bold", color ="black"))
p_LPS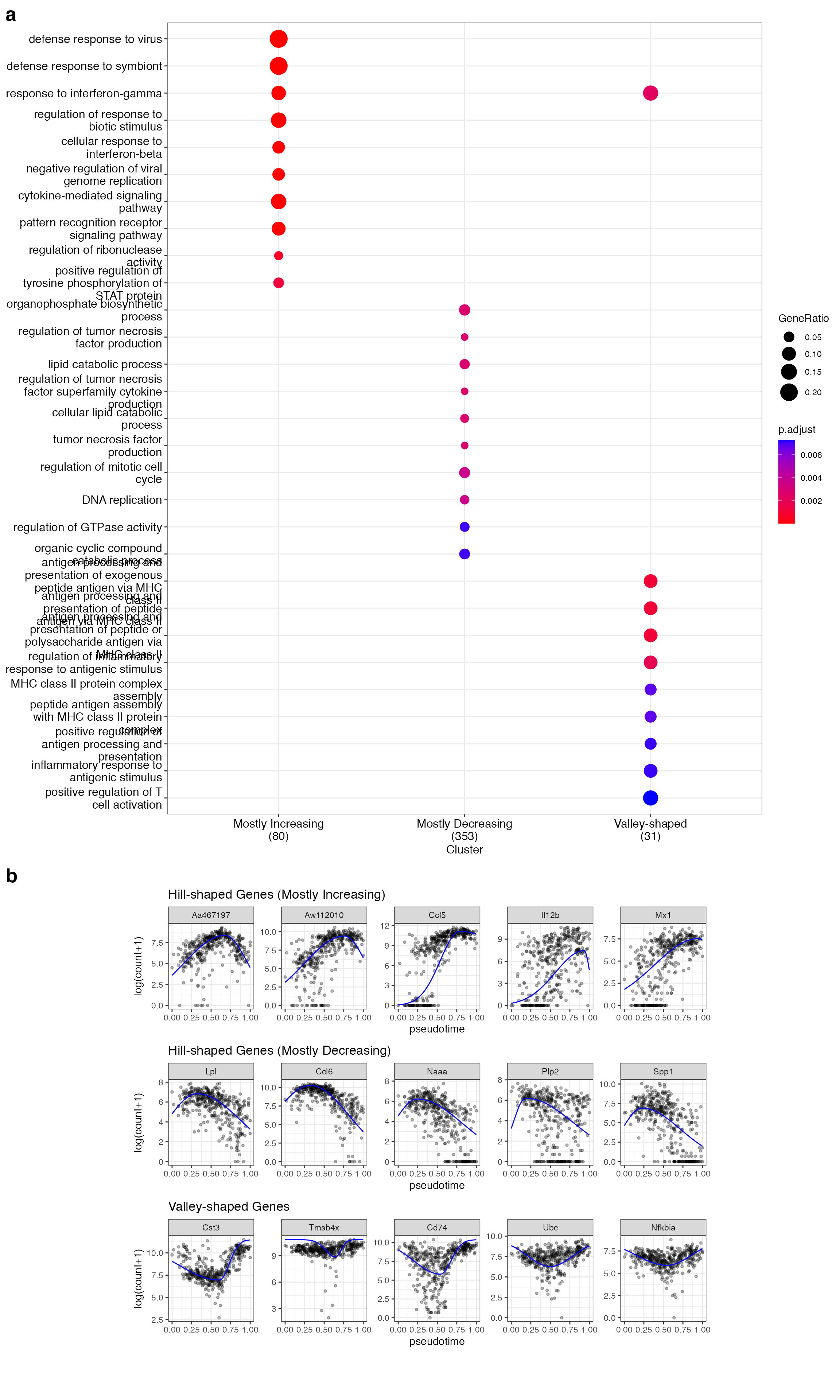

In the LPS dataset, the top enriched GO terms are different among the three gene types: Mostly increasing, Mostly decreasing, and Valley-shaped.This meets our expectation and are biologically interpretable. Notably, the hill-shaped & mostly increasing genes are related to immune response processes, showing consistency between their expression trends (activation after the LPS stimulation) and functions (immune response). Further, the visualization of example genes in the three types is shown in (b). We observe that the scGTM’s fitted trends agree well with the data. In conclusion, the scGTM can help users discern genes with specific trends by its trend-informative parameters.